Three Unusual Dice    |  Double Whammy    |   Efron Dice    |   Three Player Games  |   Grime Dice  |   A Gambling Game

Non-transitive Dice James Grime

We present a set of very unusual dice, and a two player game where you will always have the advantage. You can even teach your opponent how the game works, yet still win again! Finally, we will describe a new game for three players where you can potentially beat both opponents - at the same time! Watch James Grime and David Spiegelhalter demonstrate non-transitive dice in the video to the right, and read down for more details! Three Unusual Dice Here is a game you can play with a friend. It is a game for two players, with a set of three dice. These dice are not typical dice however, because instead of having the values 1 to 6, they display various unusual values. Each player picks a die. The two dice are then rolled together and whoever gets the highest value wins. Seems fair enough yet, in a game of say ten rolls, you will always be able to pick a die with a better chance of winning - no matter which die your friend chooses. And you can make these dice at home right now. Here is the set of three special dice: Each die has six faces but only two values, as follows; A: 3 3 3 3 3 6 B: 2 2 2 5 5 5 C: 1 4 4 4 4 4 It can be shown (see below) that in the long run die A beats die B, and that die B beats die C. So it appears A is the strong die and C is the weak die. So you might expect die A to beat die C; If this is the case we call the dice `transitive' because the winning property transfers via the die in the middle, die B. [1] However this is not the case. In fact, the winning property goes round in a circle - like a game of `Rock, Paper, Scissors' - with die A beating die B, die B beating die C, and die C beating die A. There is no strong or weak die, so the dice are `non-transitive'. How can this be? Let's do an example calculation and show that, in the long run, die A has a better chance of beating die B. Notice, when you roll die A there are two possible outcomes; you either roll a 3 or a 6. The probability of rolling a 3 is 5/6, while the probability of rolling a 6 is 1/6. On the other hand, die B can either roll a 2 or a 5, each with a probability of 1/2. So in total, if we roll die A and die B together, we have four possible outcomes. I can draw a tree diagram of all the possible outcomes. You find the probability of each outcome by  multiplying the probabilities along the diagram. For example, the probability of rolling a 5 with die A and a 2 with die B is 5/6 x 1/2 = 5/12. If I want to find the probability that die A wins I add up the probabilities of all the outcomes where die A beats die B. So in this case, the probability die A beats die B is 7/12 - importantly, this is more than 1/2. In the same way it can be shown that die B beats die C, and then remarkably die C beats die A. So, as long as your opponent picks first, you will always be able to pick a die with a better chance of winning, with the average winning probability being around 62%  [2] . Although known before, this set of three dice are currently sold by toy collector and consultant Tim Rowett [3] . Rowett chose this particular set of dice over all other choices of non-transitive dice because this is the optimum set. In other words, we have maximised the lowest winning probability. But that is not the only surprising thing about these particular dice. Double Whammy After a few defeats your friend may have become suspicious, but all is not lost. Once you've explained how the dice beat each other in a circle, challenge your friend to one more game. This time you will choose first, in which case your opponent should be able to pick a die with a better chance of winning. But let's increase the stakes, and increase the number of dice. This time each player rolls two of his chosen die, so that the player with the highest total wins. Maybe two dice means your opponent has just doubled their chances of winning. But not so because, amazingly, with two dice the order of the chain flips! In other words, the chain reverses so the circle of victory now becomes a circle of defeat. Now, die A beats die C, die C beats die B, and die B beats die A. Allowing you to win the game again! The average winning probability with two dice is around 57%  [4] . A word of warning though; although the probability that die A beats die C is greater than 1/2, it is a slim victory. In the short term, say less than 20 rolls, the effect is closer to 50-50, so you will still need some luck on your side! Efron Dice The idea for non-transitive dice has been around since the early 1970s [5] . However, the remarkable reversing property is not true for all sets of non-transitive dice, for you do need to pick your values carefully. For example, here is another famous set of non-transitive dice; it is a set of four non-transitive dice known as `Efron Dice' and invented by the American statistician Brad Efron:   This time the dice use values 0 to 6. Each die has values: A: 3 3 3 3 3 3 B: 2 2 2 2 6 6 C: 1 1 1 5 5 5 D: 0 0 4 4 4 4 As before, the dice form a circle where die A beats die B, die B beats die C, die C beats die D, and die D beats die A, and they each do so with a probability of 2/3. Efron Dice are optimal, in the sense that the lowest winning probability achieves the theoretical upper bound. We also have two pairs of dice opposing each other on the circle. In fact die B beats die D, but die A and die C each have a 50-50 chance of winning, with neither die dominating [6] . Unfortunately, the player picking die A will not have a very exciting game, with all the values being the number 3. Also, this chain does not display the remarkable property of flipping when you double the number of dice [7]. It is said the successful American investor Warren Buffett is a fan of non-transitive dice. When he challenged his friend Bill Gates to a game, with a set of Efron dice, Bill became suspicious and insisted Warren choose first. Maybe if Warren had chosen a set with a reversing property he could have beaten Gates - he would just need to announce if they were playing a one die or two dice version of the game after they had both chosen. Three Player Games I wanted to know if it was possible to extend this to make a three player game, a set of dice where two of your friends may pick a die each, yet you can pick a die that has a better chance of beating both opponents - at the same time! It turns out there is a way. The Dutch puzzle inventor M. Oskar van Deventer [8] came up with a set of seven non-transitive dice, with values from 1 to 21 [9] . Here two opponents may each choose a die from the set of seven, and yet there will be a third die with a better chance of beating each of them. The probabilities are remarkably symmetric with each arrow on the diagram illustrating a probability of 5/9. But there is still the question of whether you can beat your two opponents at the same time.  If the dice were regular fair dice, with two competing dice having a 50-50 chance of victory (ignoring draws), then the chance of beating two opponents at the same time would stand at just over 25%. It isn't exactly 25% because beating one player is not independent of beating the other player - when you roll a high number you are likely to beat both! However, these dice are not fair. Even though you have the advantage against both opponents, beating both players is still a challenge, with the probability of doing so standing around 39%. This set of seven dice form a complete directed graph. In the same way, a four player game would require 19 dice. 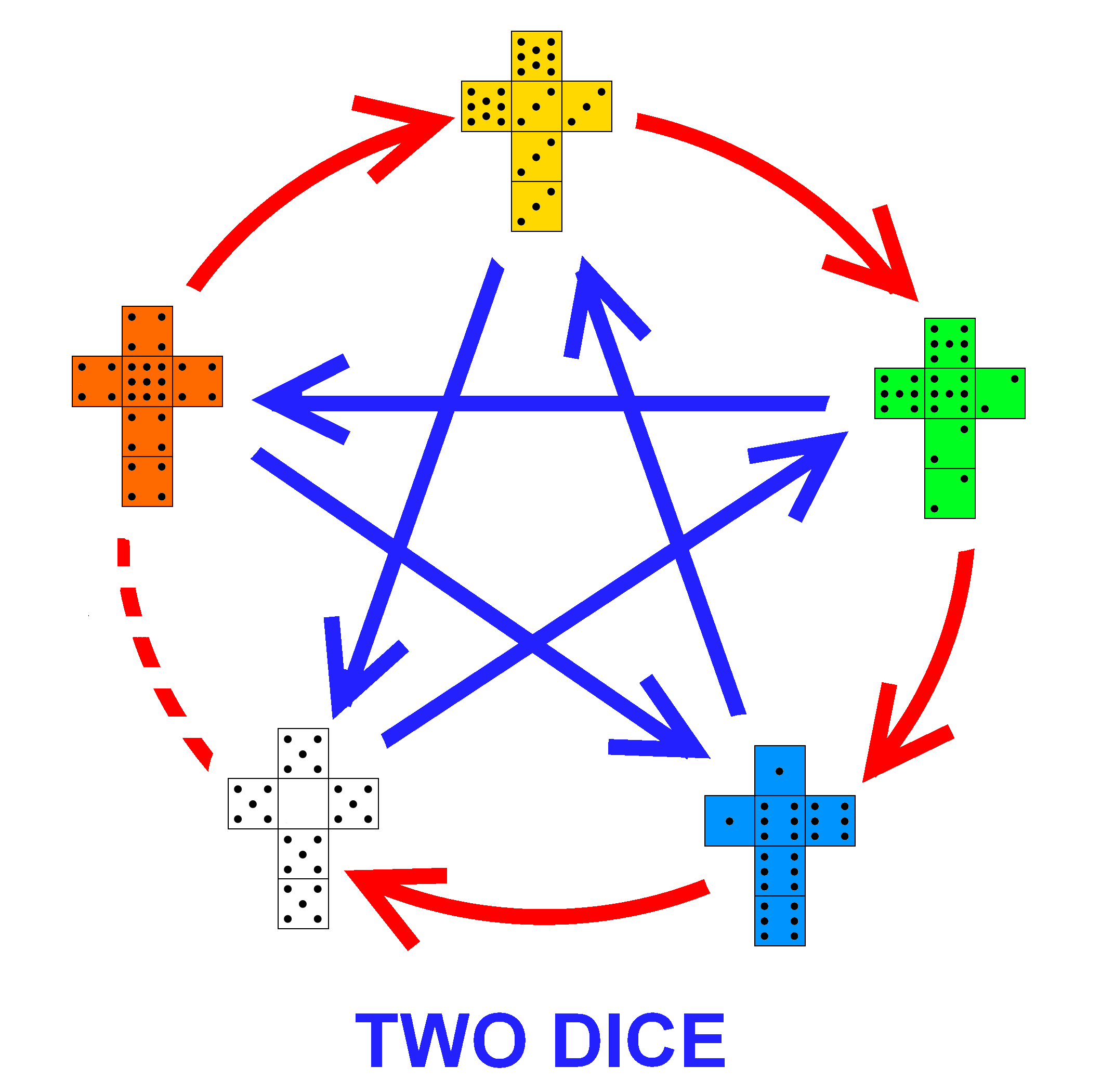It is not known if such a set exists. However, if it is possible to construct a set of non-transitive dice with a reversing property, then it might be possible to have a three player game with fewer than seven dice. And potentially such a set might improve our chances of beating two players at the same time. I have devised such a set below. Grime Dice  Here is a set of five non-transitive dice: These dice use values from 0 to 9, as follows; A: 4 4 4 4 4 9 B: 3 3 3 3 8 8 C: 2 2 2 7 7 7 D: 1 1 6 6 6 6 E: 0 5 5 5 5 5 This set of five dice is similar to other sets of dice we have seen, in that we have a chain where A>B>C>D>E>A. However, within that we now have a second chain, where A>C>E>B>D>A. The average winning probability for one die is 63%  [10] . If our original set of three non-transitive dice was like a game of `Rock, Paper, Scissors', this diagram is closer to the related, but more extreme, non-transitive game `Rock, Paper, Scissors, Lizard, Spock' [11] . With two dice the first chain stays the same. But the second chain now flips so A>D>B>E>C>A. The average winning probability for two dice is 59% [12] . I will add one caveat: although it is desirable that E>A with two dice, in the short term (say less than 20 rolls) the effect is closer to 50-50, with neither die dominating. In all other cases your choice of die will give you a healthy advantage over your two opponents. Overall, the average winning probability is 61%. Here is how you play the game against two opponents: invite each player to pick one of the dice, but do not volunteer the rules of the game at this point. When the two other players have made their choice, you may now make your choice - including whether you and your opponents will be playing the one die or two dice version of the game. As before we play a game of say 10 rolls and, no matter which dice your opponents choose, there will always be a die with a better chance of beating each player. For example, if one opponent chooses die B and the other opponent chooses die C, then you should pick die A and play the one die version of the game. Then, according to the first diagram above, you will have a better chance of beating each opponent. On the other hand, if one opponent chooses die C and the other opponent chooses die E, then you should pick die B and play the two dice version of the game. Then, according to the second diagram above, you can expect to beat each opponent again. A Gambling Game But, can we expect to beat the two other players at the same time? Well, we have certainly improved the odds, with the average probability of beating both opponents now standing around 44% - a 5% improvement over Oskar Dice, and a 19% improvement over fair dice! [13]  So, if the odds of beating two players isn't over 50% then how do we win? Consider the following gambling game: Challenge two friends to a dice game, where you will play your two opponents at the same time. If you lose you will give your opponent £1. If you win your opponent gives you £1. So, if you beat both players at the same time you win £2; if you lose to both players you lose £2; and if you beat one player but not the other then your net loss is zero. You and your friends decide to play a game of 100 rolls. If the dice were fair then each player will expect to win zero - each player wins half the time and loses half the time. However, with Oskar Dice, you should expect to beat both players 39% of the time, and lose to both players 28% of the time, which will give you a net profit of £22. But even better, with Grime Dice, you should expect to beat both players 43.8% of the time, but only lose to both players 22.7% of the time, giving you an average net profit closer to £42! (And possibly the loss of two former friends). This set is the best set of five non-transitive dice with these properties that I have found. You may also like to consider subsets of Grime Dice. There are 5 subsets of three dice and 5 subsets of four dice that make non-transitive chains. For example, the dice A, C and E form a non-transitive subset of three dice. In fact, this is just a copy of Rowlett Dice with different numbers. This subset also has the reversing property of Rowlett Dice, and the slim victory in the two set version of Rowlett dice explains the slim defeat displayed in the two set version of Grime Dice. This subset is optimal in the sense that the lowest winning probability reaches its theoretical upper bound, with an average winning probability of 62%. Any subset of four Grime Dice make a non-transitive chain, with the subsets A, B, C and E and A, C, D, E both having an average winning probability of 2/3. However, these subsets are not copies of Efron Dice and are not optimal, although they do have the same average winning probability as Efron Dice. I invite you to try out these games yourself [14]. They are easy to make by either writing on blank dice, or modifying some old dice. They are also inexpensive to buy and you can get the set of three Rowett Dice and the set of four Efron Dice from Grand Illusions . Try them out on your friends and enjoy your successes and failures! Footnotes: [1] Other examples of transitivity: If a, b and c are real numbers then if a > b and b > c, then we know a > c. For example, if 9 > 4.6 and 4.6 > 5/3 then 9 > 5/3. If a, b and c are integers such that a stictly divides b (with no remainder) and b strictly divides c, then we know a strictly divides c. For example, if 3|15 and 15|60 then 3|60. The last two relations are transitive. On the other hand, if a,b and c are integers such that a+b > 7 and b+c > 7, we cannot deduce that a+c > 7. This relation is not transitive.  [2] In full the probabilities are: P(A > B) = 7/12, P(B > C) = 7/12 and P(C > A) = 25/36. [3] Tim Rowett introduced this set of non-transitive dice at the Gathering for Gardner V (2002). They can be bought exclusively from Grand Illusions http://www.grand-illusions.com [4] This time the full probabilities are: P(A > C) = 671/1296 (a slim victory!), P(C > B) = 85/144, and P(B > A) = 85/144. [5] Gardner, M. "Mathematical Games: The Paradox of the Nontransitive Dice and the Elusive Principle of Indifference." Sci. Amer. 223 , 110-114, Dec. 1970. [6] Efron Dice: P(A > B) = 2/3, P(B > C) = 2/3, P(C > D) = 2/3, P(D > A) = 2/3, P(A > C) = 1/2 and P(B > D) = 5/9 [7] The probabilities for two sets of Efron Dice are: P(A > D) = 5/9, P(B > A) = 5/9, P(B > C) = 5/9, P(C > D) = 5/9, P(B>D) = 11/27, P(D > B) = 0, P(B = D) = 16/27 (a draw), P(A > C) = 1/4, P(C > A) = 1/4, P(A = C) = 1/2. There is no chain like before. [8] M. Oskar van Deventer on Youtube: http://www.youtube.com/user/OskarPuzzle [9] Mathematical Association of America on Oskar dice: http://www.maa.org/editorial/mathgames/mathgames_07_11_05.html [10] Grime Dice, one die version: P(A > B) = 13/18, P(B > C) = 2/3, P(C > D) = 2/3, P(D > E) = 13/18, P(E > A) = 25/36; P(A > C) = 7/12, P(B > D) = 5/9, P(C > E) = 7/12, P(D > A) = 5/9, P(E > B) = 5/9. [11] Home of Rock, Paper, Scissors, Lizard, Spock: http://www.samkass.com/theories/RPSSL.html Or if that isn't extreme enough, how about Rock, Paper, Scissors with 101 gestures; RPS-101 http://www.umop.com/rps101.htm [12] Grime Dice, two dice version: P(A > B) = 7/12, P(B > C) = 5/9, P(C > D) = 5/9, P(D > E) = 7/12, P(E > A) = 625/1296(*); P(A > D) = 56/81, P(B > E) = 56/81, P(C > A) = 85/144, P(D > B) = 16/27, P(E > C) = 85/144. (*)This is a slim defeat! However, when rounded to the nearest whole number, the expected number of wins is the same as 50% for anything less than 28 trials. Also, 95% of the time we expect the number of wins to be plus/minus two standard deviations from the mean. When we take this into account, the effect is little different from 50%. [13] In the ideal three player game, we would like the average probability of beating two players to be over 50%. This would mean, on average, each winning die should beat another with a probability of over 70%. It has been shown that for three non-transitive dice, the die with the smallest winning probability has an upper bound, namely the Golden Ratio Conjugate Φ = 0.618. The upper bound may not necessarily be obtainable, and it will depend on the number of sides the dice have. You will come closest to the upper bound when the number of sides is a Fibonacci number. Rowett Dice are the optimum set of three six-sided dice. For four non-transitive dice the upper bound is 2/3 - making Efron dice optimal in this sense, since the die with the smallest winning probability obtains its upper bound. For five dice the upper bound is 0.692. This sequence of upper bounds increases with the number of dice and converges to 3/4. Naturally, if the weakest die achieves the upper bound then the average winning probability will be even higher. References; The Paradox of Nontransitive Dice, Richard P. Savage, Jr. The American Mathematical Monthly, Vol. 101, No. 5 (May, 1994), pp. 429-436 http://www.jstor.org/stable/2974903 and; S. Trybula, On the paradox of n random variables, Zastos. Mat. 8 (1965), 143-154. [14] For the very keen, here's a set to try that uses mathematical constants: A: 1 1 1 1 1 π ; B: Φ Φ Φ e e e; C: 0 φ φ φ φ φ ; where  e is Euler's Number, φ is the Golden Ratio and Φ is the Golden Ratio Conjugate. Do these dice form a non-transitive set? What about with two dice, does the order reverse as before?